Regularization: Ridge (L2), Lasso (L1), and Elastic Net regression

이번 포스팅에서는 Regularization의 필요성과 대표적인 모델, Ridge (L2), Lasso (L1) 그리고 Elastic Net regression을 정리합니다.

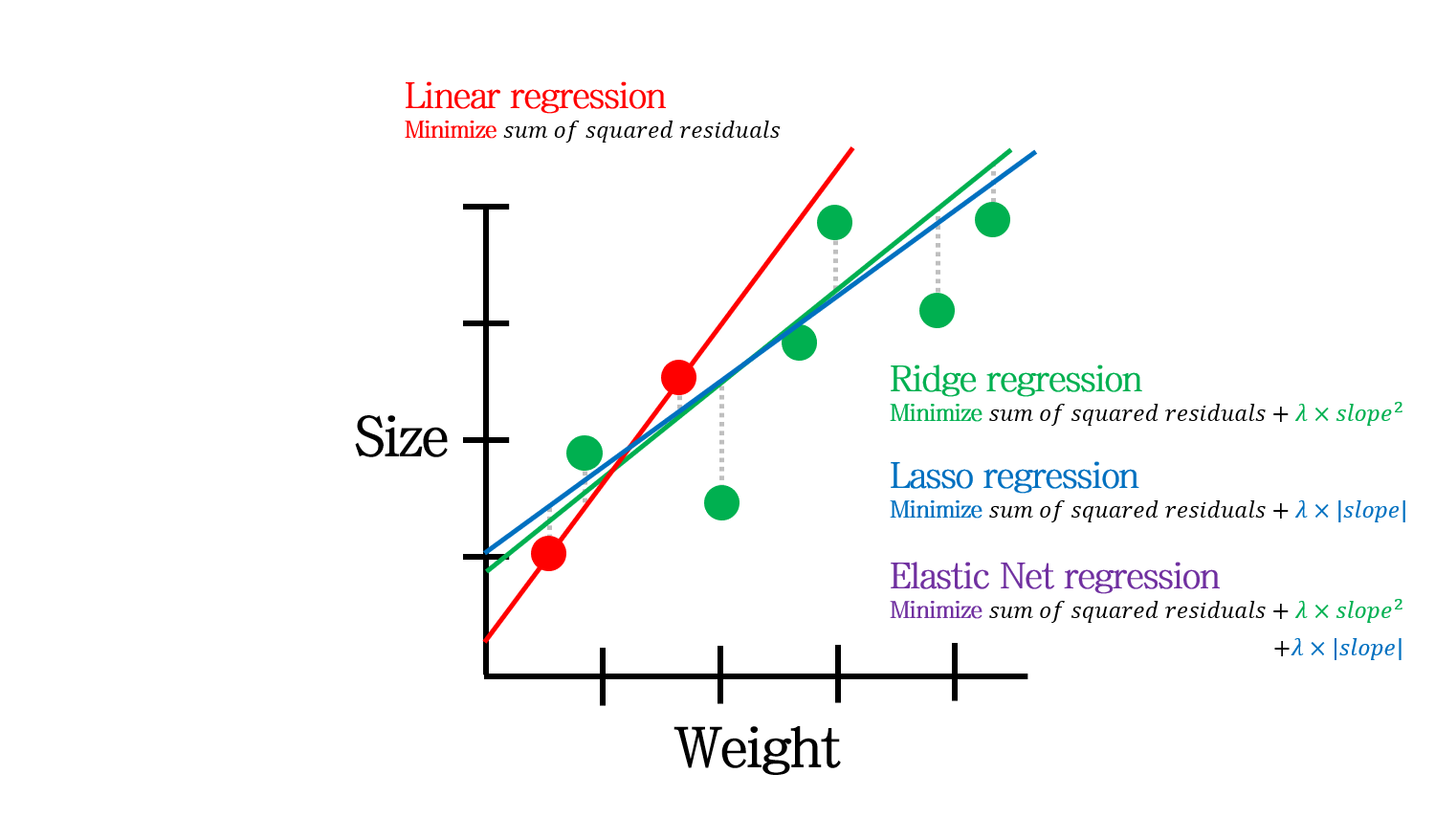
위 그림은 오늘 포스팅에서 다룰 내용을 나타냅니다.

Regularization

Regularization을 속담 (?)으로 비유하면 살을 내주고 뼈를 취한다로 표현하면 좋을 것 같습니다.

기계학습 용어로 표현하면, Bias를 조금 높이는 대신, Variance를 확 낮춘다 정도로 말할 수 있습니다.

간단한 예시로 Regularization을 정리해봅시다.

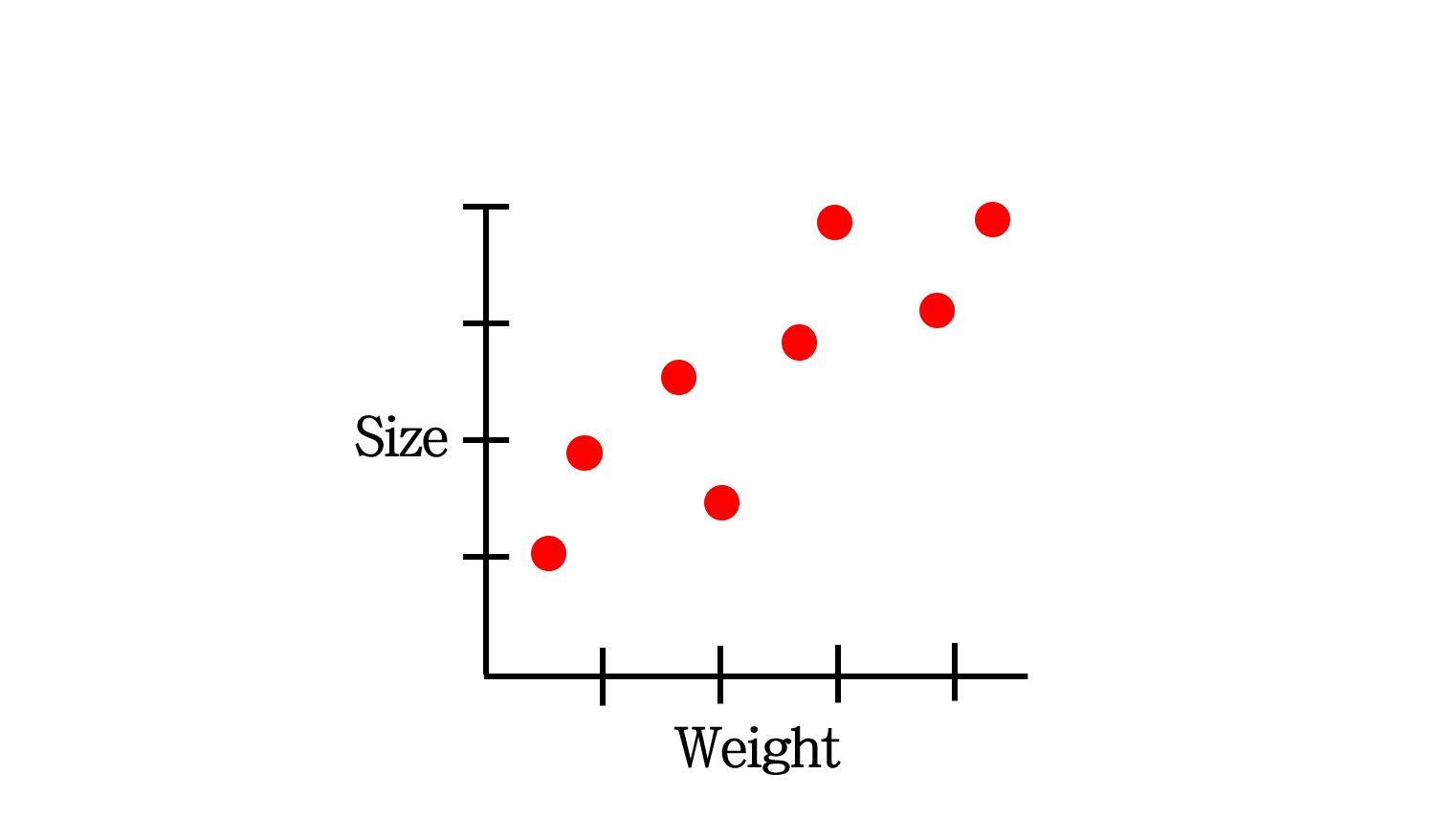
위 예시는 쥐의 몸무게와 사이즈의 관계를 나타내기 위한 데이터입니다. 몸무게만으로 사이즈를 계산하기 위해 선형 모델을 세운다고 합시다.

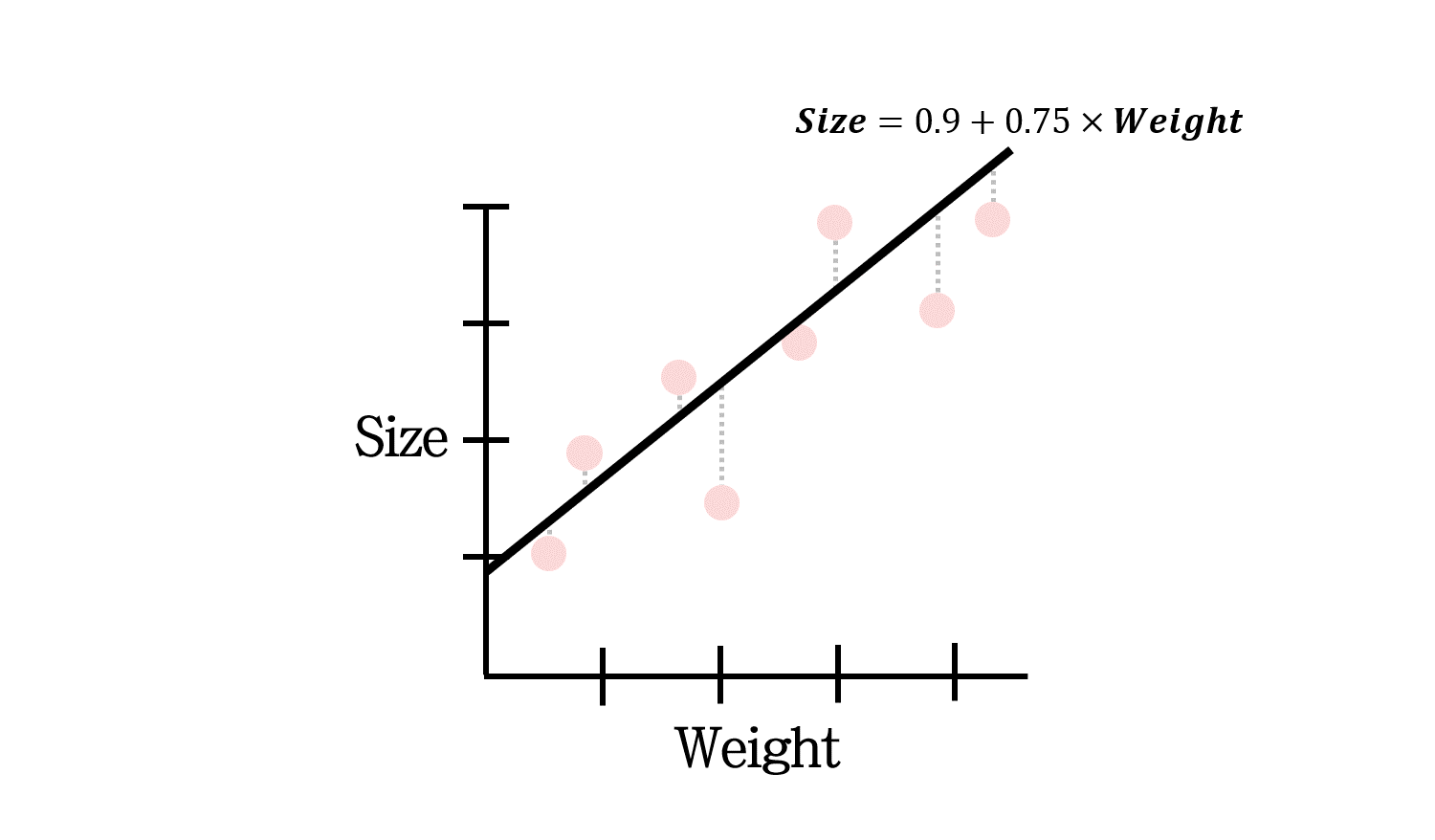
해당 선형 모델은 이렇게 나타낼 수 있을 것입니다. 그런데 만약 데이터 수가 너무 적다면 어떨까요?

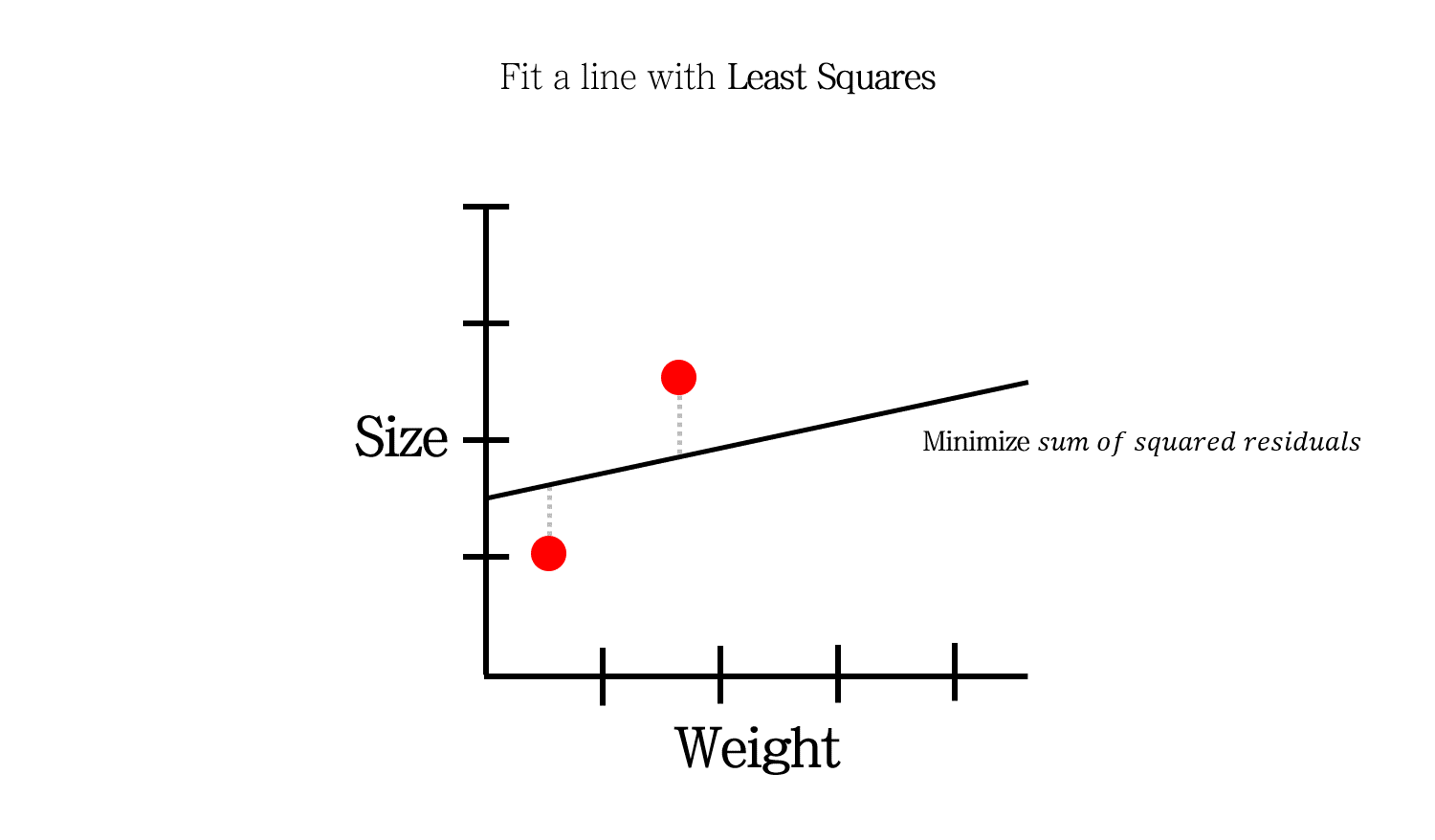
이 문제를 풀기 위해 우리는 \(sum\; of\; sqaured\; residuals\)을 최소화해서 least square 해를 찾습니다.

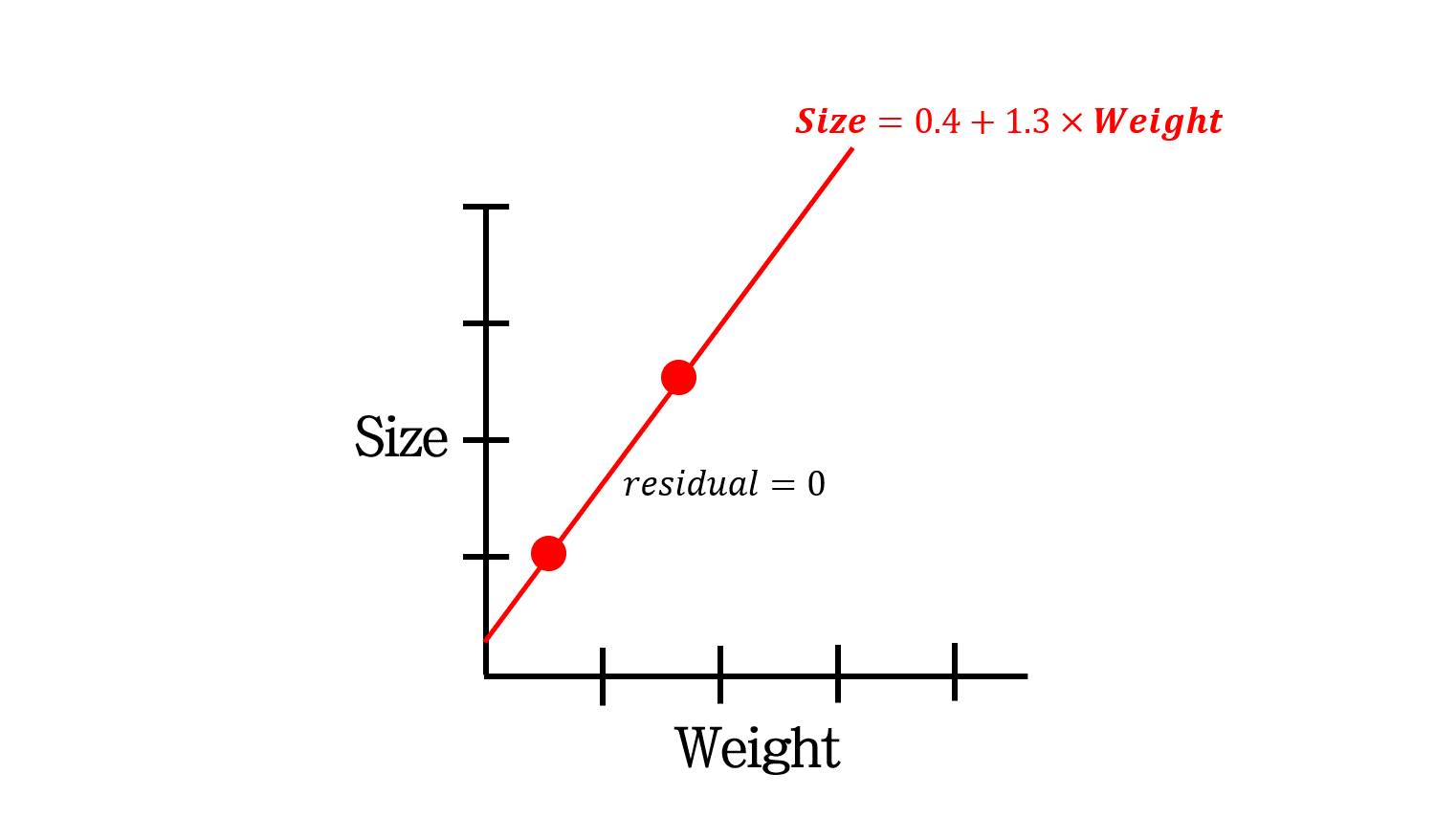
이렇게 말이죠.

그런데말입니다. 새로운 데이터가 들어와도 이 모델이 성립할까요?

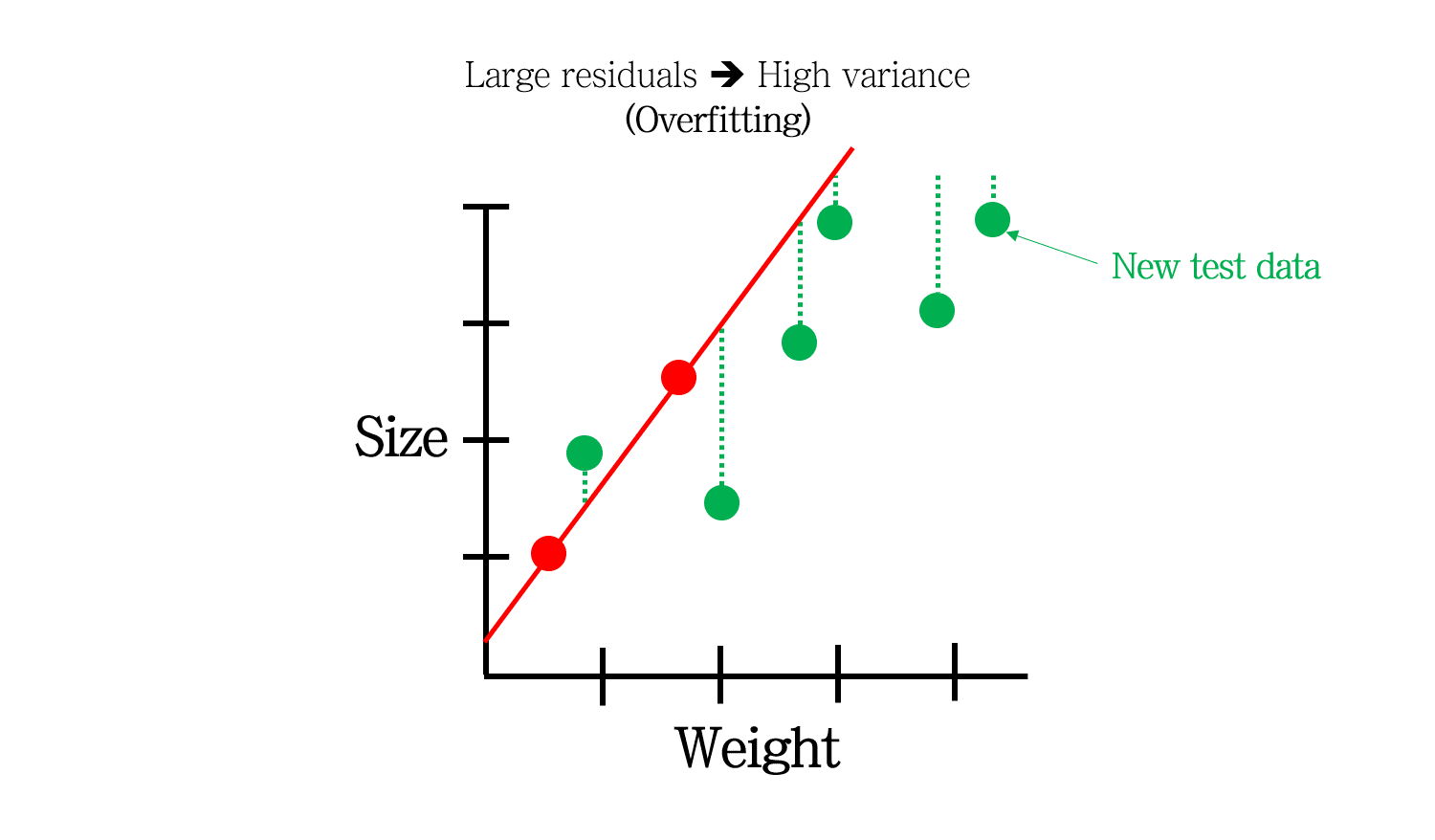
초록색으로 나타난 새로운 모델이 들어왔을 때, 이 모델은 상당한 오차를 낼 것입니다. 즉, 이 모델은 Variance가 높다고 말할 수 있습니다.

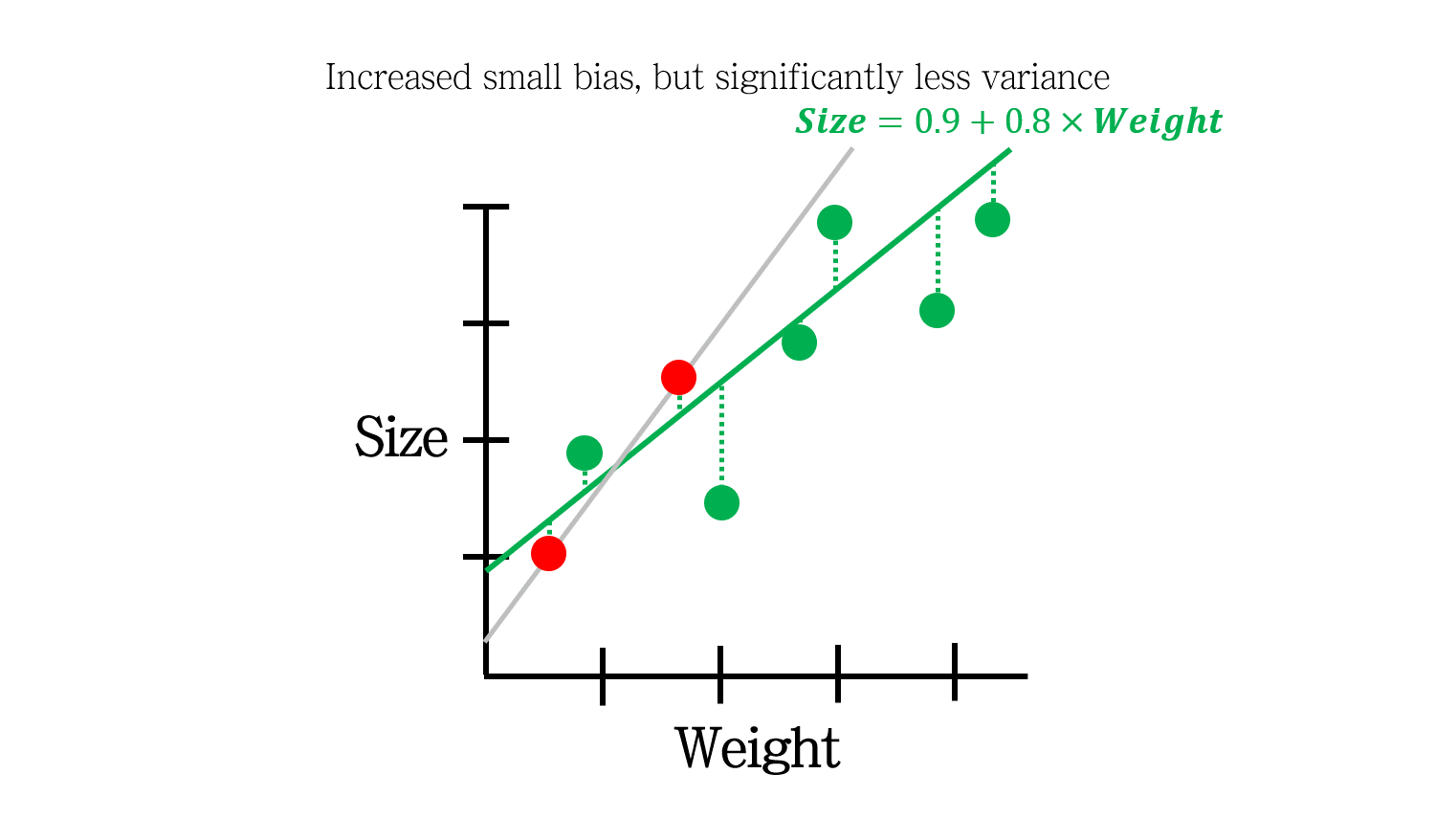
Regularization은 이럴 때 사용됩니다. 초록색 실선은 training 데이터에 조금의 error (bias)가 있는 대신, test 데이터에 대한 error (variance)가 상대적으로 더 적습니다. 결과적으로 error의 총량이 더 적어지는 효과를 냅니다.

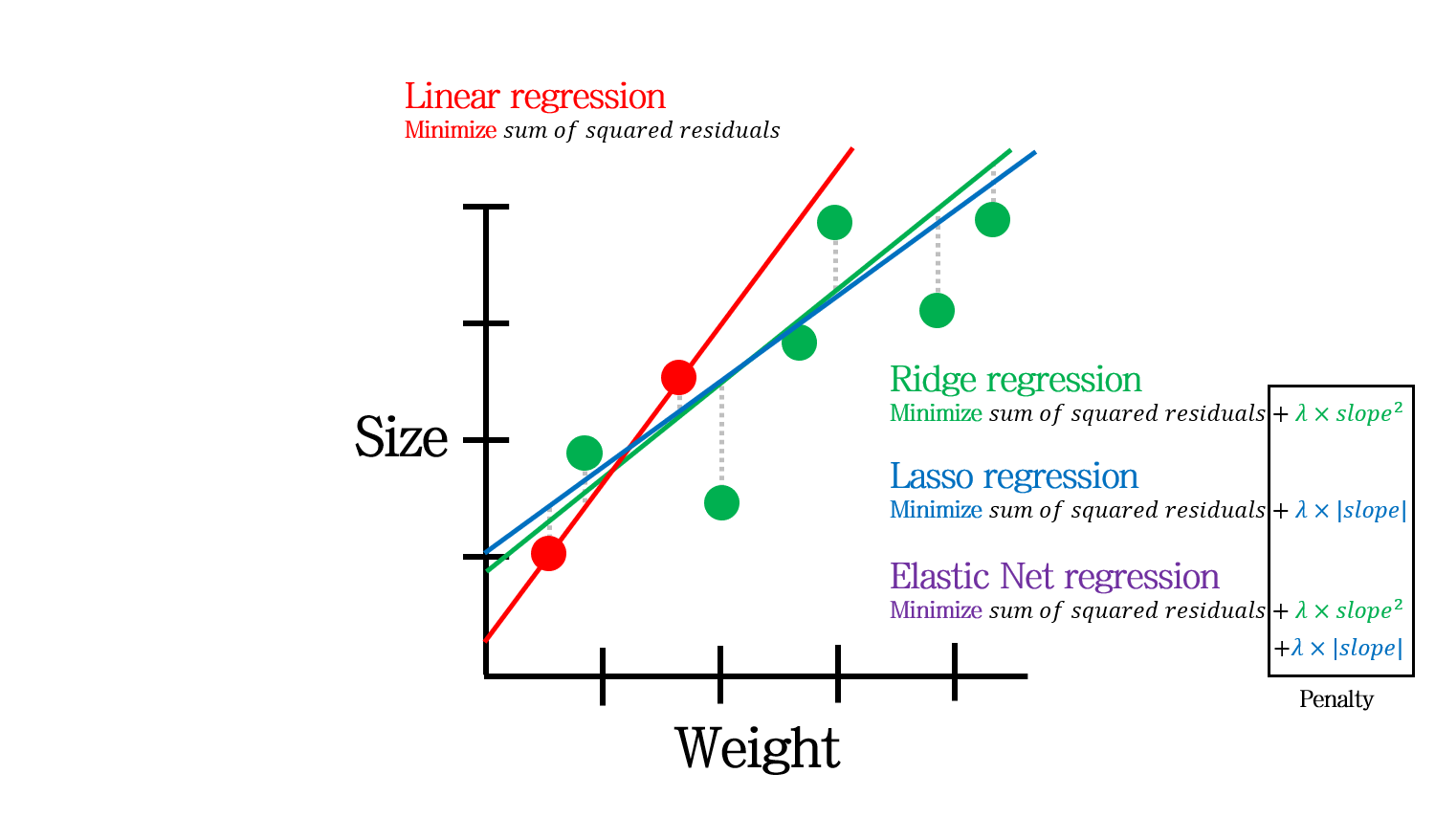
Regularization의 종류에는 오늘 정리할 Ridge (L2) regression, Lasso (L1) regression이 대표적입니다. 그 외에도 Elastic Net 등이 있습니다. 각 모델은 회귀식의 weight 값에 penalty를 주는데, 이 penalty의 방식에 따라 종류가 나뉩니다.

Ridge (L2) regression

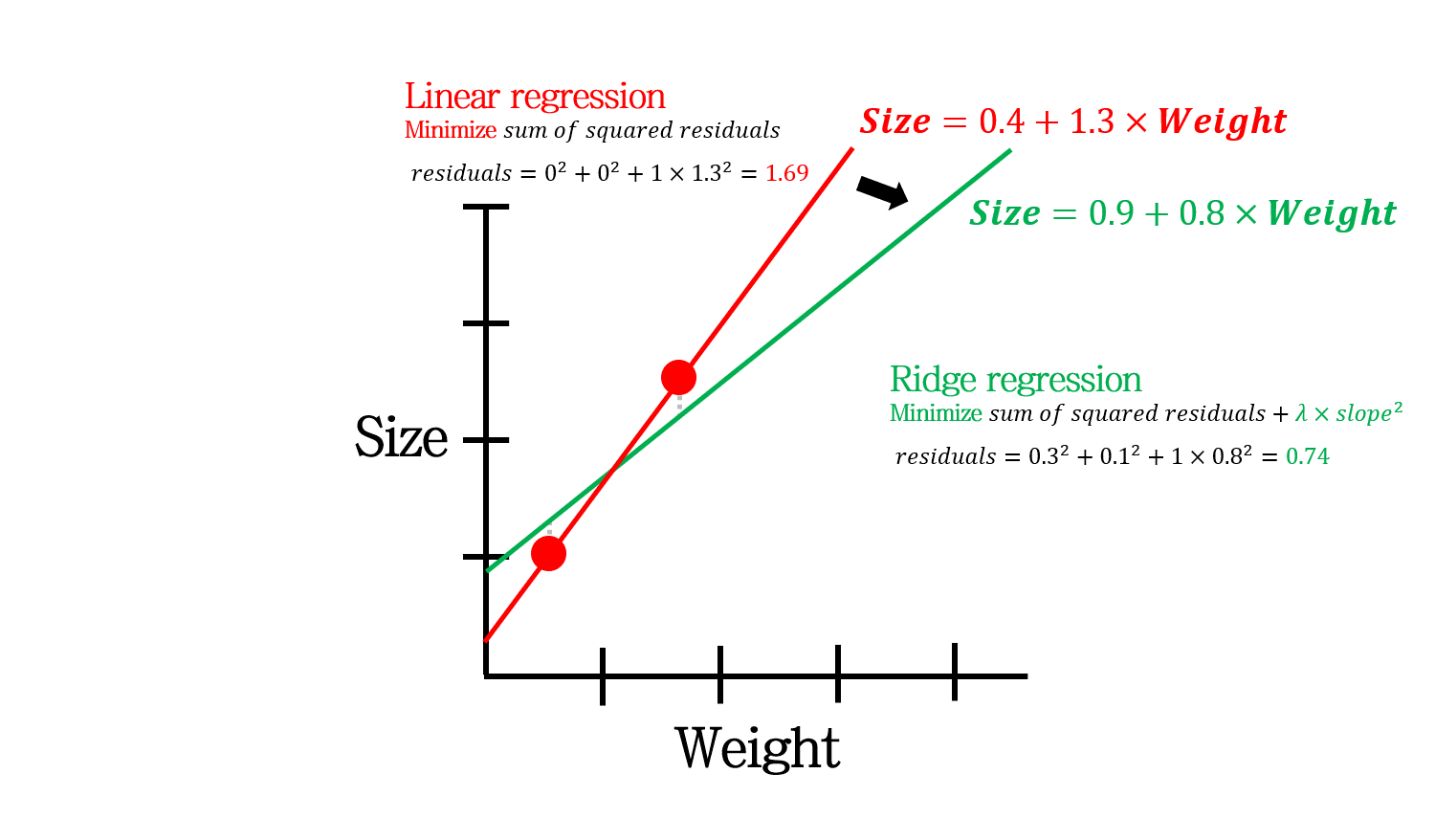
Ridge는 penalty의 종류로 weight의 제곱합을 사용합니다. 여기에 penalty의 가중치인 \(\lambda\)를 곱해줍니다.

\(\lambda=0\)이라고 할 때, 위 예시에서 빨간색 실선 (Linear regression의 해)은 training data 에 대한 residual이 0임에도 penalty만으로 1.69라는 error가 나온 반면, 초록색 실선 (Ridge regression의 해)은 0.74의 error가 나온 것을 확인할 수 있습니다.

즉, penalty term의 추가로 인해 최적해가 바뀌는 것을 확인할 수 있습니다.

higher \lambda on Ridge regression

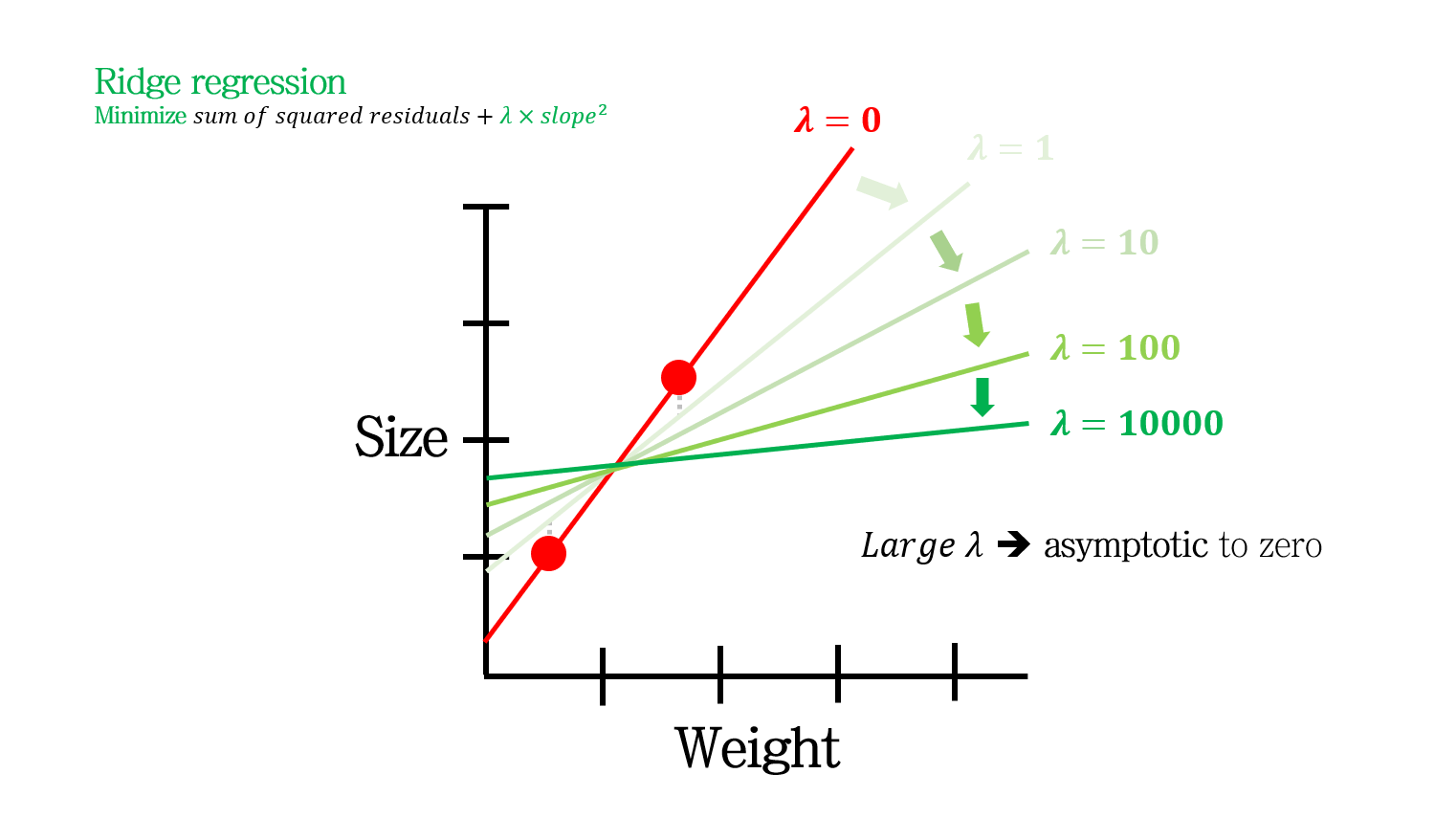
\(\lambda\)가 크다는 것은 더 강력한 제한 조건을 부여하겠다는 말입니다. 따라서 \(\lambda\)가 커짐에 따라 slope (변수의 weight)는 점점 작아지면서 0에 근사하게 됩니다.

with discrete variable

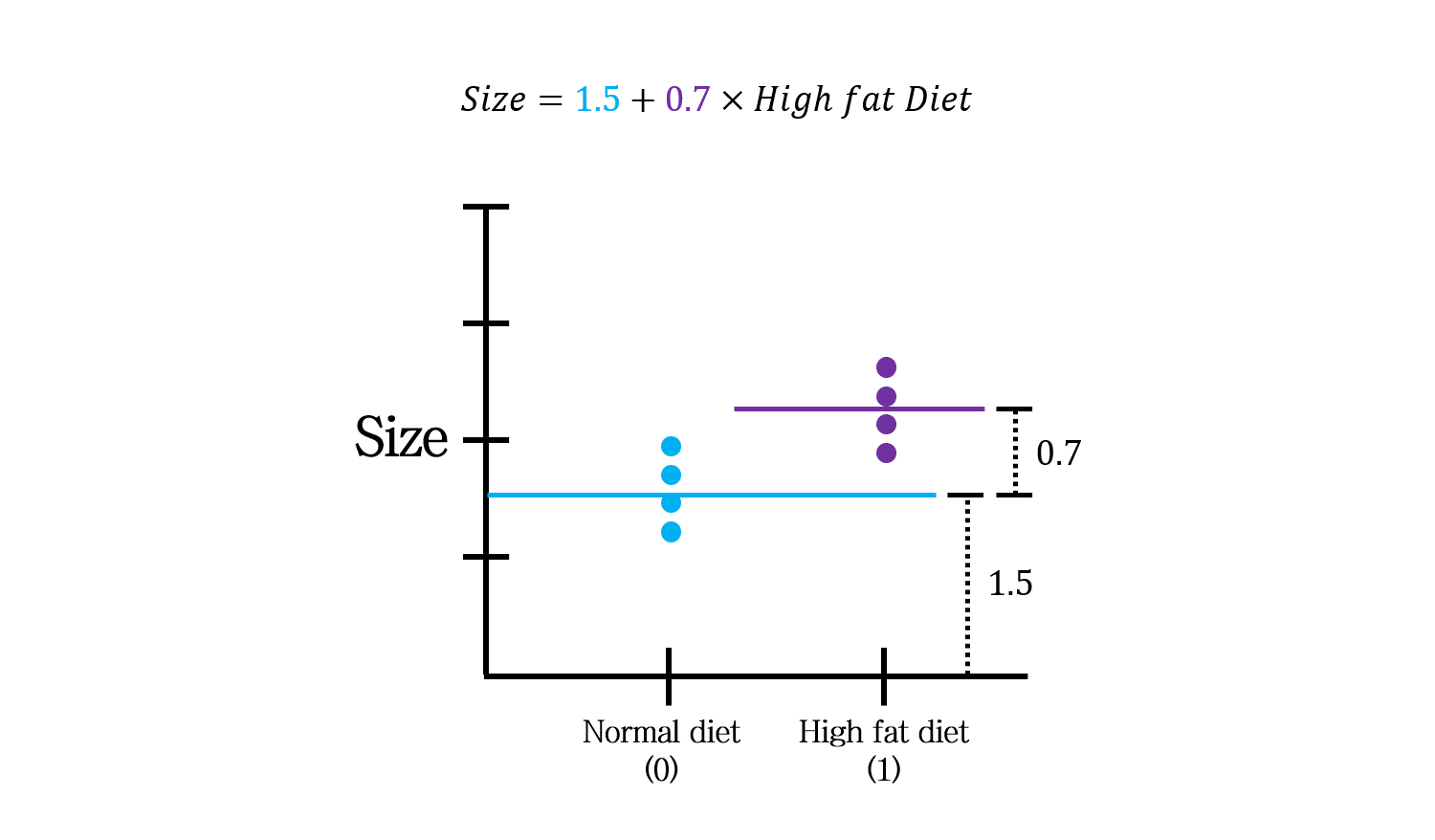
연속형 변수뿐 아니라 범주형 변수로도 Ridge regression이 가능합니다.

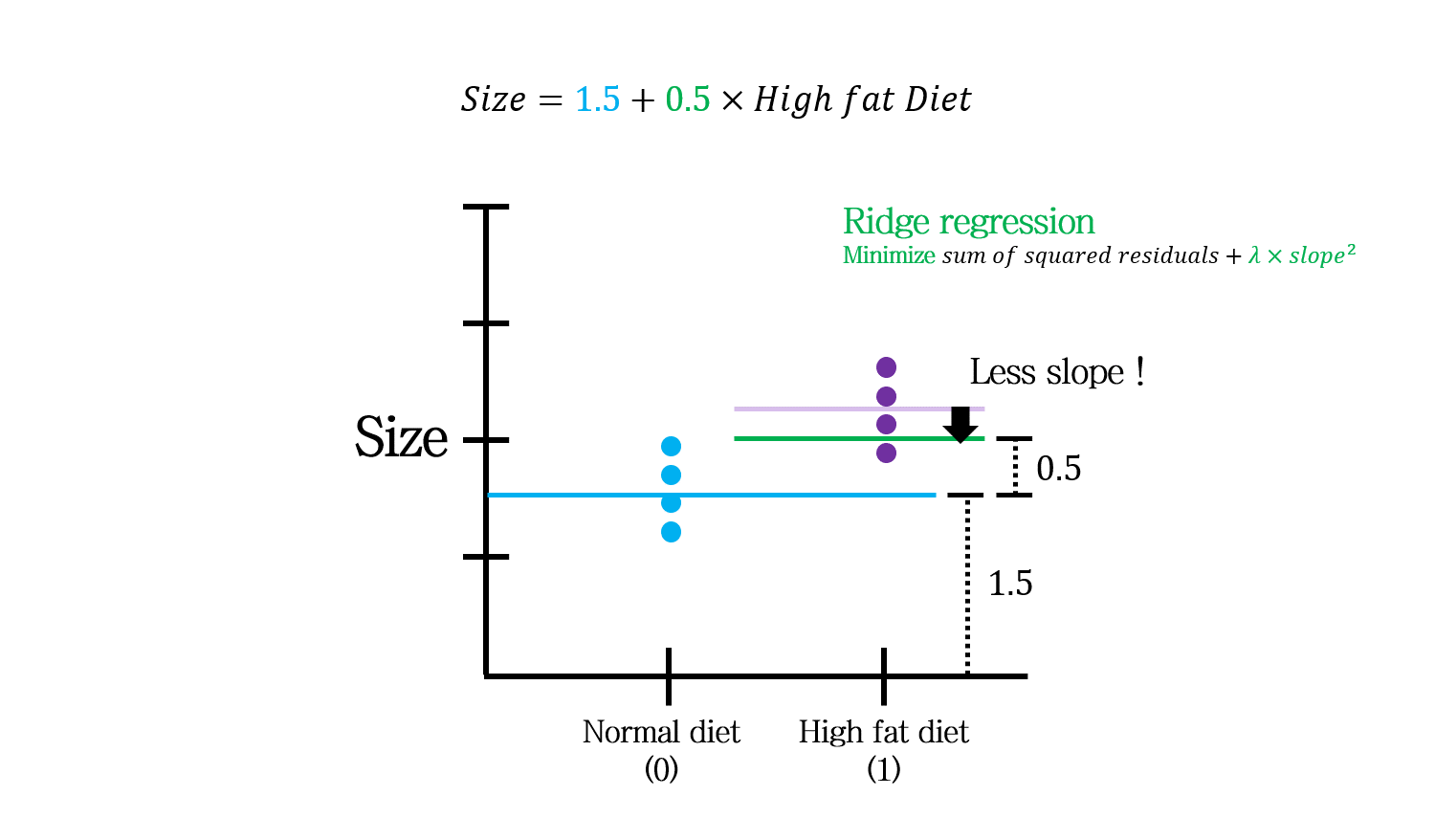
이런 식으로 표현되는 것으로 이해할 수 있겠죠.

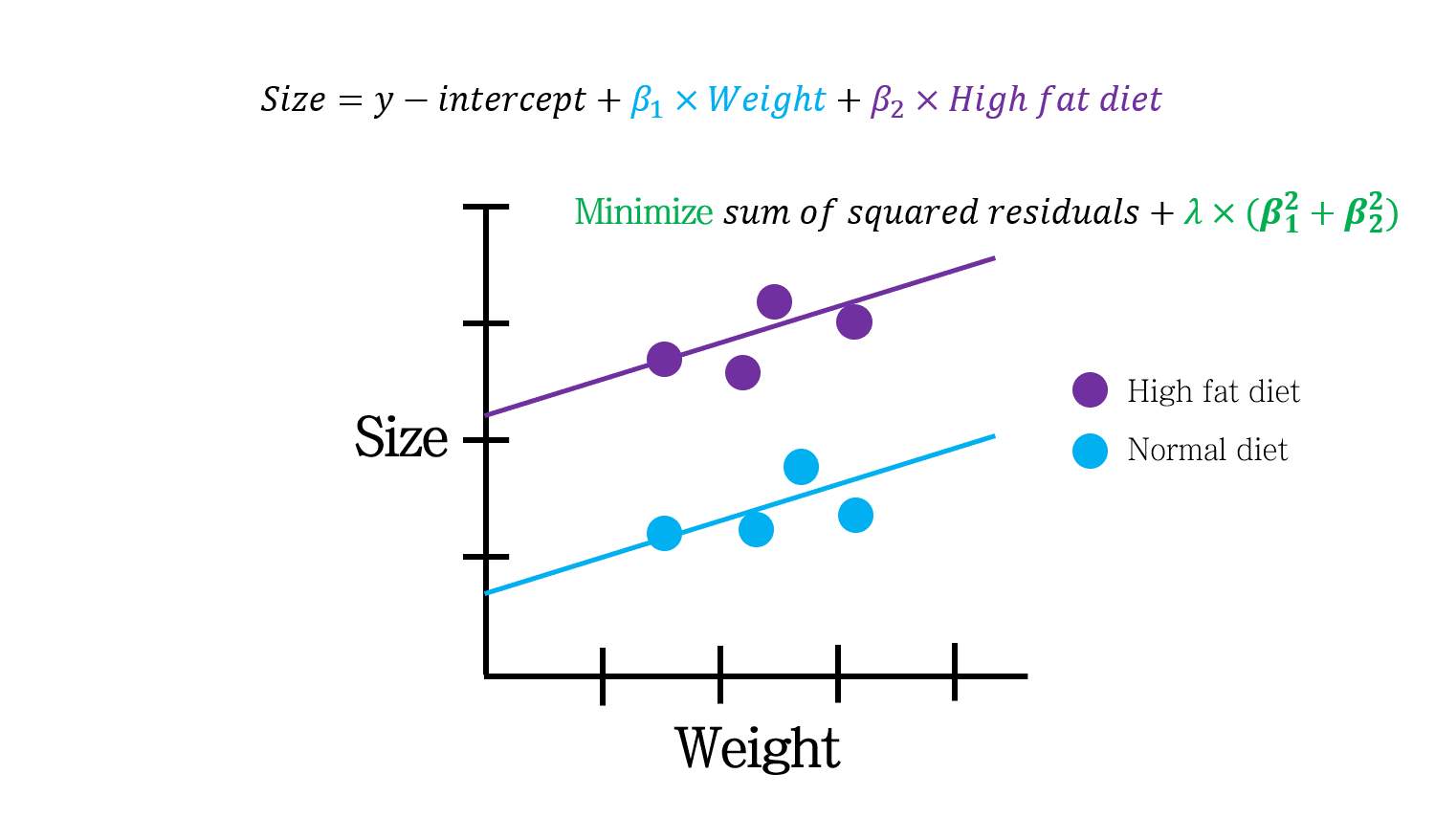
연속형 변수와 범주형 변수가 함께 있는 경우는 위 그림처럼 이해하면 됩니다.

Lasso (L1) regression

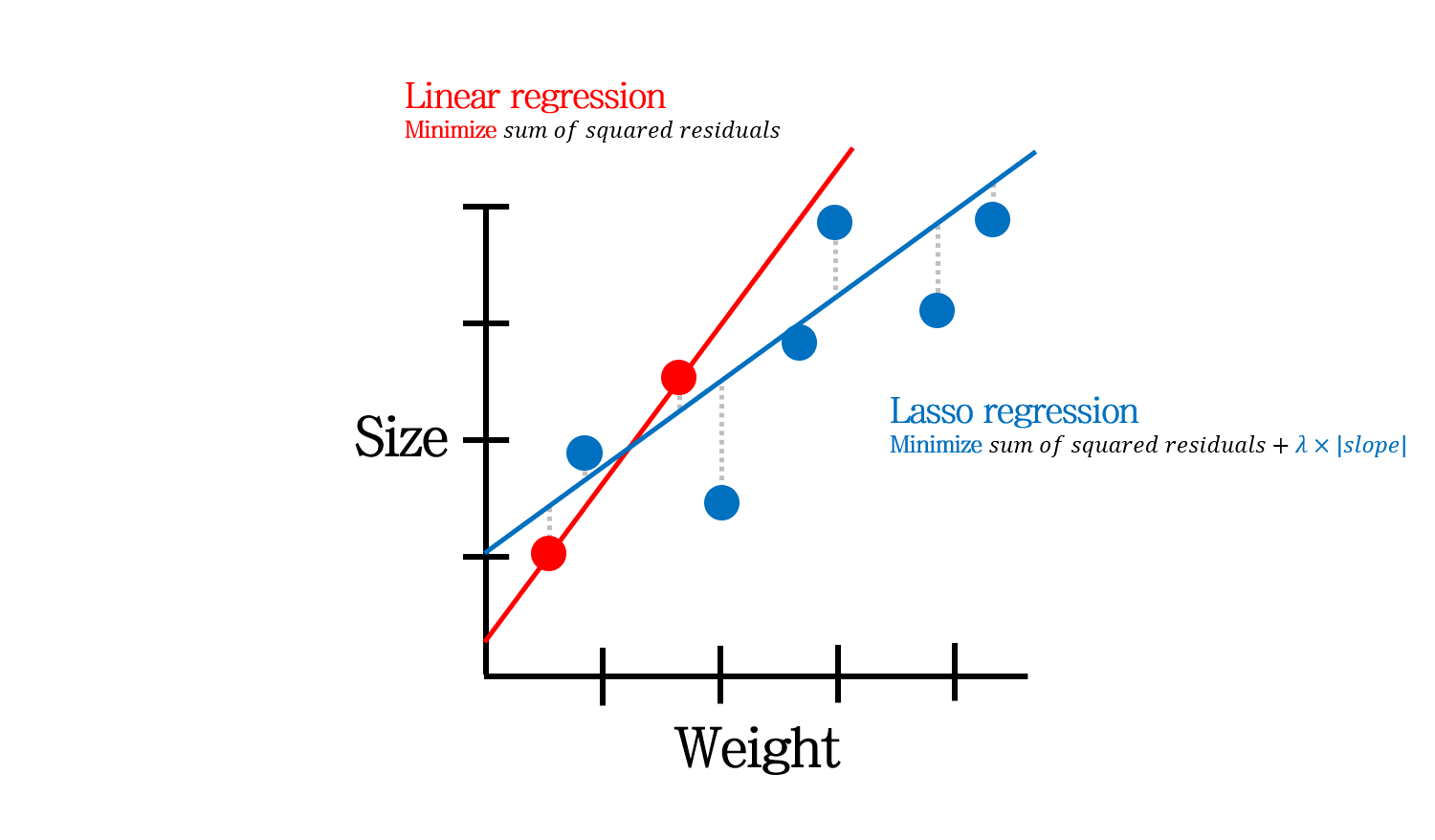
Lasso regression은 또 다른 regularization 방법입니다. penalty term으로 weight의 제곱 합이 아닌, 절대값 합을 사용합니다.

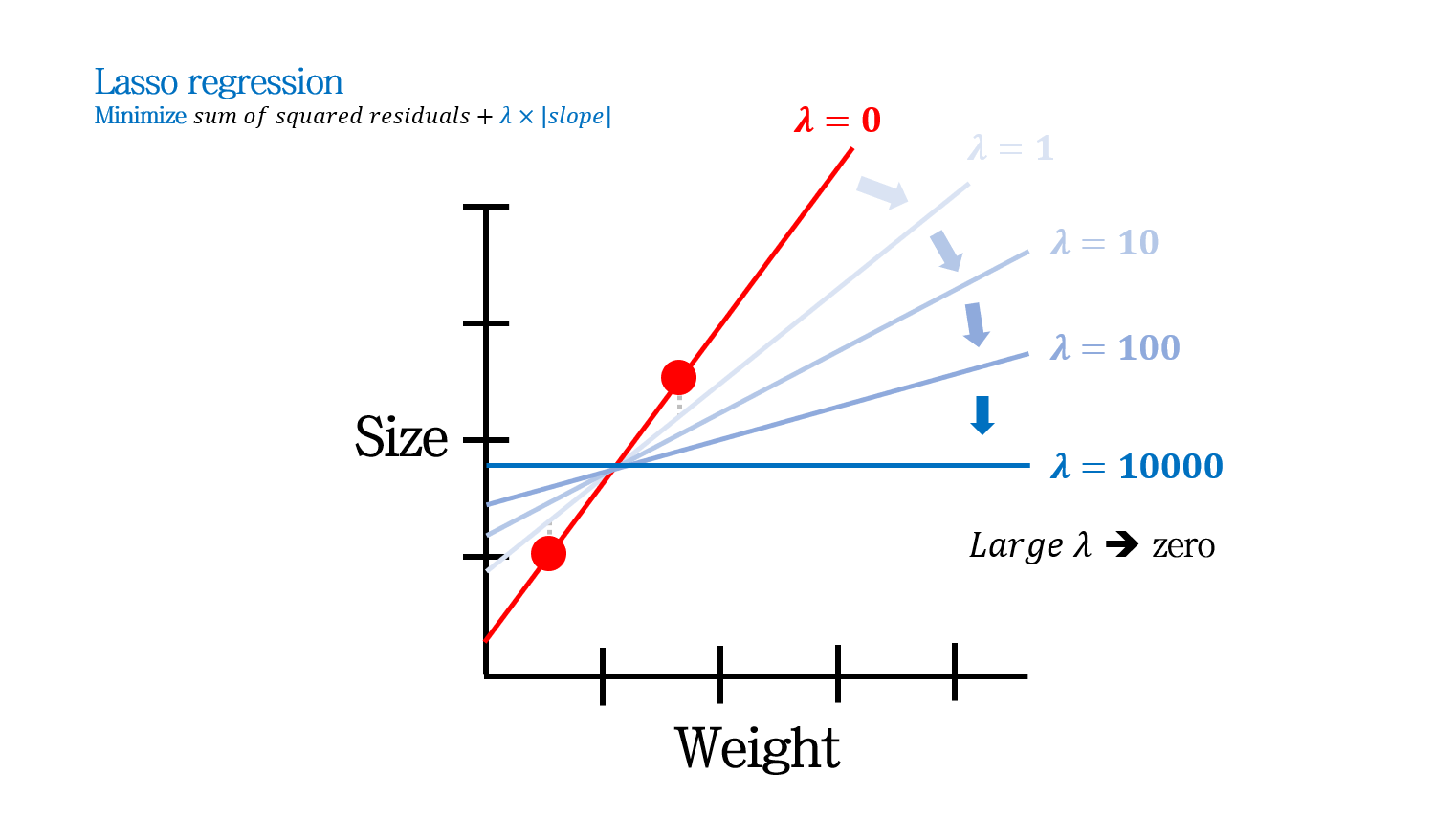
Lasso도 Ridge와 마찬가지로 \(\lambda\)가 커짐에 따라 slope (변수의 weight)는 점점 작아집니다. 그런데, Lasso에서는 \(\lambda\)가 많이 커지면 일부 slope (weight)가 0이 되는 현상이 나타납니다. 추가적인 설명은 후술하도록 합니다.

Lasso도 Ridge와 마찬가지로 범주형변수에도 사용할 수 있습니다.

Ridge VS Lasso

Ridge와 Lasso는 매우매우매우 비슷한 regularization 방법입니다. 두 모델의 가장 중요한 차이점은 \(\lambda\)에 따라 일부 slope가 0에 근사하는지 (Ridge), 또는 아예 0이 되는지 (Lasso) 입니다.

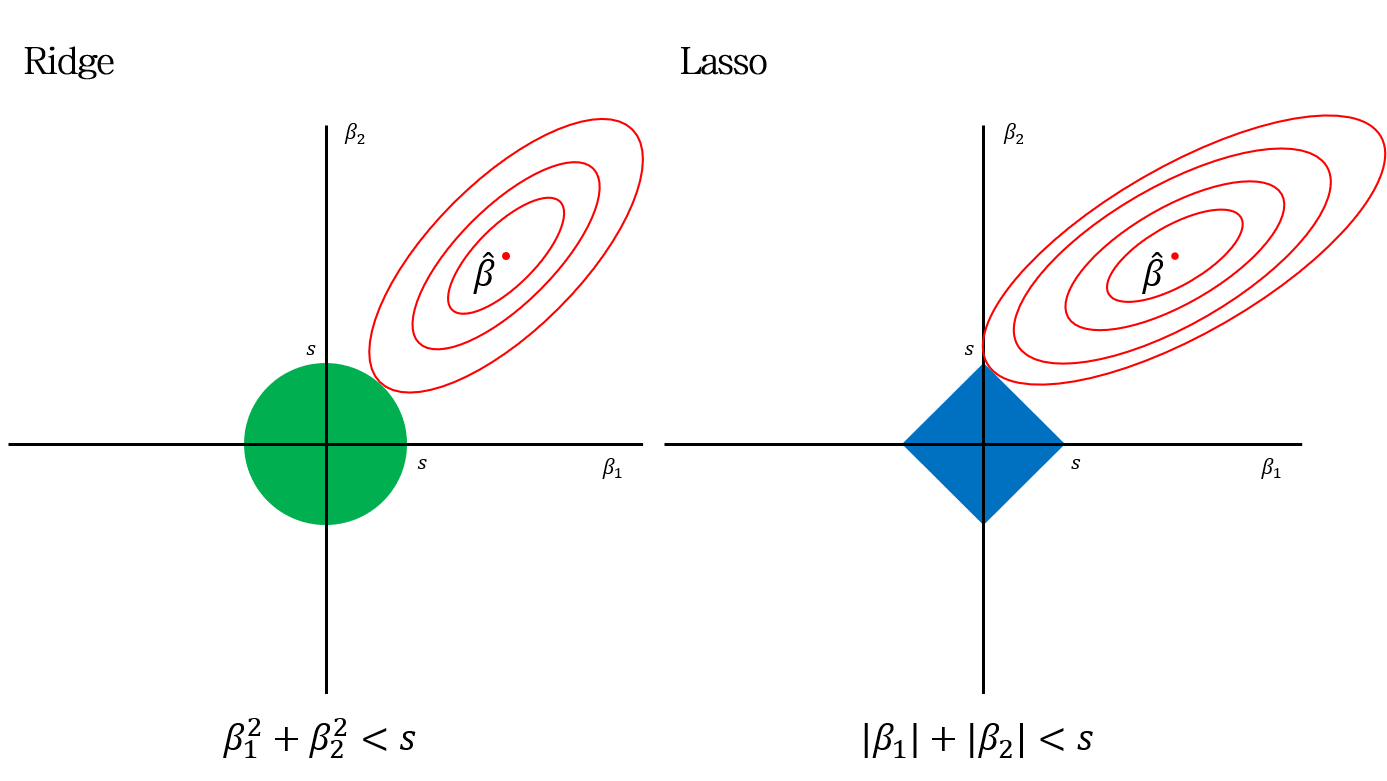
이는 두 모델을 기하학적으로 이해할 때 가장 쉽게 이해할 수 있습니다.

두 연속형 변수로 이루어진 회귀모델을 생각해봅시다. 위 그림에서 \(\beta_1\)와 \(\beta_2\)는 slope (weight)를 의미합니다. 또한 \(\hat{\beta}\)는 least square를 갖는 지점이고, 빨간 등고선은 동일한 RSS를 나타내는 선입니다.

좌측 Ridge의 초록색 원과 우측 Lasso의 파란색 마름모는 각 모델의 제약범위, 즉 \(\beta_1^2+\beta_2^2<s\)와  \(\lvert\beta_1\rvert+\lvert\beta_2\rvert<s\)영역을 의미합니다. 각 모델은 해당 제약범위 내에서, 가능한 가장 작은 RSS를 갖는 값으로 계수를 추정합니다.

여기서 \(s\)가 작다는 것은, slope들에 제약 조건을 더 많이 건다는 것입니다.. 즉 \(\lambda\)가 큰 것을 의미합니다.

반면, \(s\)가 충분히 큰 것은 \(\lambda\)가 작은 것을 의미합니다. \(s\)가 충분히 커서 \(\hat{beta}\)의 점을 포함하게 된다면, 모델은 일반적인 linear regression의 least square와 같은 값을 추정하게 됩니다

따라서 Ridge 또는 Lasso에서 추정되는 계수 (\(\beta_1, \beta_2\)는 주어진 제약범위와 가장 작은 RSS등고선이 만나는 지점의 값이 됩니다.

Ridge에서 제약범위와 RSS 등고선이 만나는 지점의 slope 값들은 0이 되지 않습니다. \(\lambda\)가 커질 때 (\(s\)가 작아질 때)도 slope들은 0에 가까운 값은 되어도, 0 자체가 될 수는 없습니다.

반면, Lasso에서는 제약범위와 RSS 등고선이 만나는 지점이 마름모의 모서리가 될 확률이 높습니다 (확률이라고 하는 것은 \(\lambda\)에 따라 모서리에서 만나는 것이 아닐 수도 있기 때문입니다. 사각형을 키워보면 직관적으로 이해할 수 있습니다). \(\lambda\)가 커질 때 (\(s\)가 작아질 때)도 아예 0 값을 갖는 slope가 나올 확률이 높아집니다.

Feature selection via Lasso

Lasso의 이 특징은 Feature selection에 활용될 수 있습니다. 변수의 가중치를 0으로 만들어 결과 추정에 필요 없는 변수를 제거해버리는 효과입니다.

Elastic Net Regression

앞서 Ridge와 Lasso를 비교해보았습니다. 두 모델은 매우 비슷한 Regularization 모델이지만, Penalty term이 다릅니다. 두 모델 중 어떤 모델을 사용해야할 지 모르겠을 때는 두 종류의 Penalty term이 합쳐진 Elastic Net을 써보는 것도 방법이 될 수 있습니다.

Elastic Net은 Ridge와 Lasso 각각의 Penalty 가중치로 \(\lambda_2\)과 \(\lambda_1\)를 사용합니다.

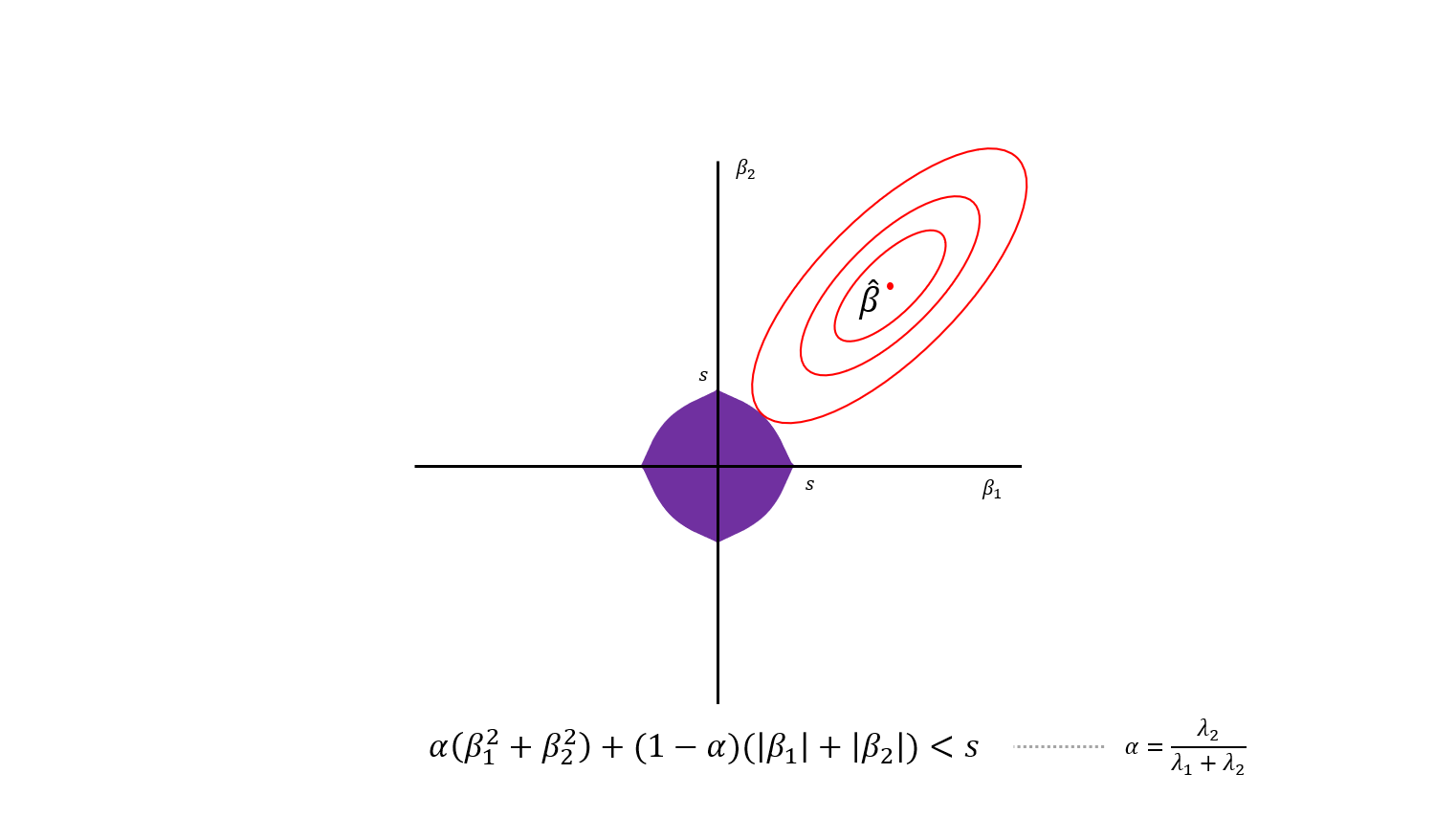
기하학적으로 생각해보면 이런 모양의 제약범위를 갖는 모델로 생각할 수 있습니다.

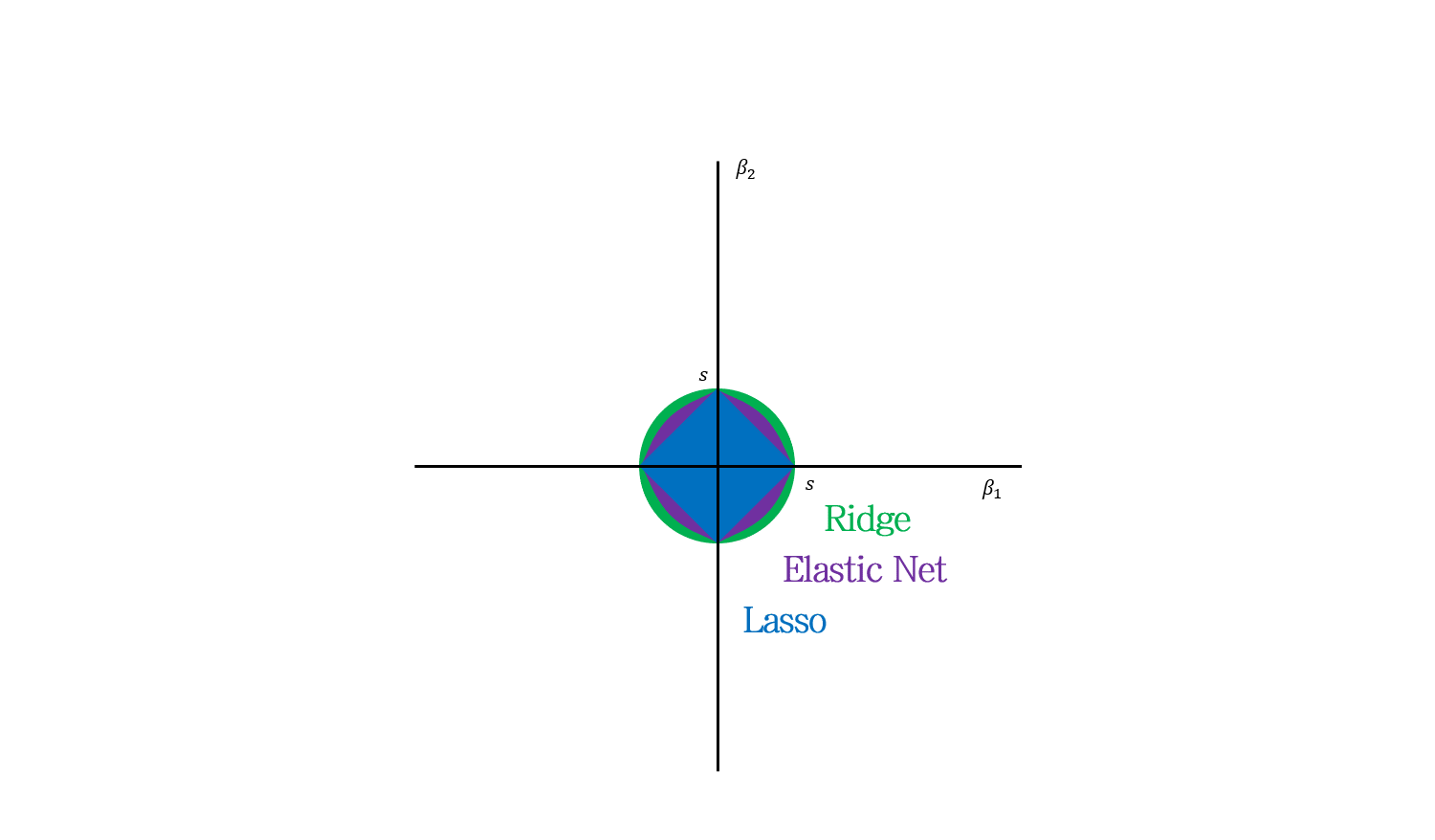
Ridge와 Lasso를 합쳤더니 마름모와 원 중간의 무언가가 된 모습. 직관적이네요.

Selection of \(\lambda\)

Ridge, Lasso, Elastic Net 모두 최적의 \(\lambda\) 값은 Cross validation을 통해 정합니다.

여러 조건의 \(\lambda\) (e.g., 0.1, 0.2, 0.3 …)로 Ridge/Lasso regression을 Cross validation을 통해 수행합니다. Elastic Net의 경우, \(\lambda_1 \times \lambda_2\)의 조합을 다 계산해봅니다.

이후 최소 error 값을 갖는 \(\lambda\)를 사용합니다.

Usage example of Ridge (Regularization)

Regularization이 필요한 이유를 되짚으면서 포스팅을 마무리합니다.

\(n\)개의 변수가 있는 식의 least square를 찾기 위해서는 \(n+1\)개의 데이터가 필요합니다 (선은 점 2개, 면은 점 3개가 필요한 것을 생각하기).

그러면 유전자처럼 수천 수만개의 변수가 있는 식을 풀기 위해서는 그만큼의 데이터가 있어야할까요? 현실적으로 그 데이터를 모으기란 쉽지 않을 겁니다.

이럴 때 Ridge regression은 weight에 penalty를 부과하여 적은 수의 샘플로 overfitting을 피해 나름의 최적의 해를 찾을 수 있게합니다.

---

Reference

Regularization Part 1: Ridge (L2) Regression
Regularization Part 2: Lasso (L1) Regression
Regularization Part 3: Elastic Net Regression